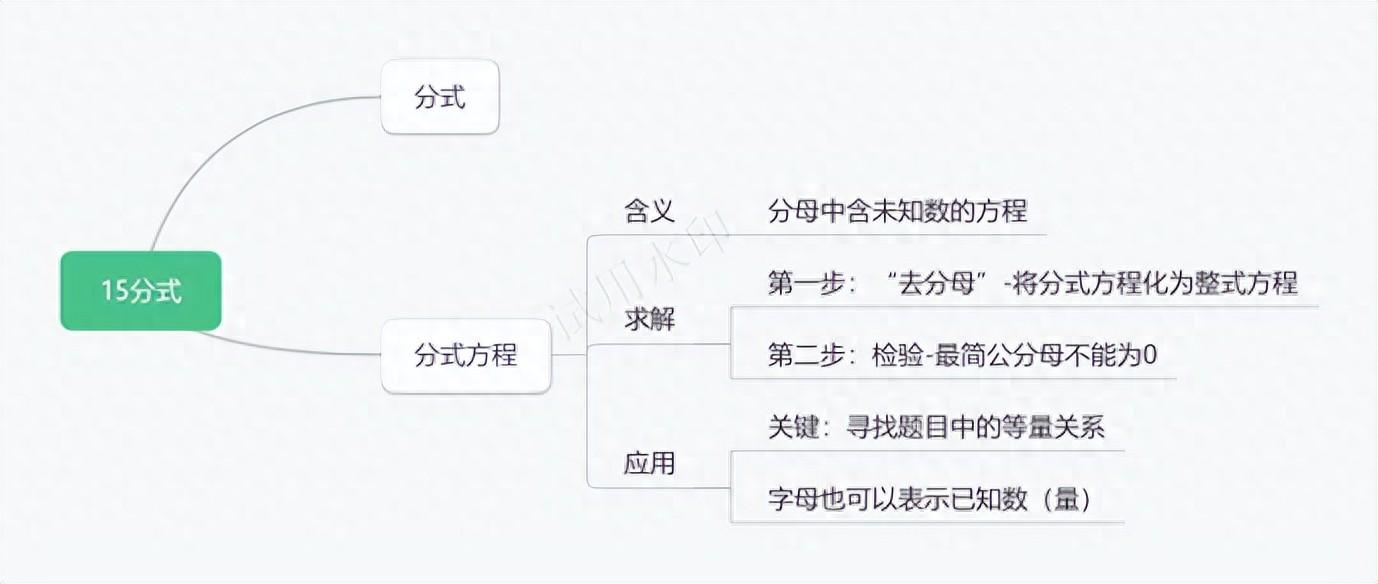
15.3分式方程
一、含义:分母中含未知数的方程叫做分式方程。
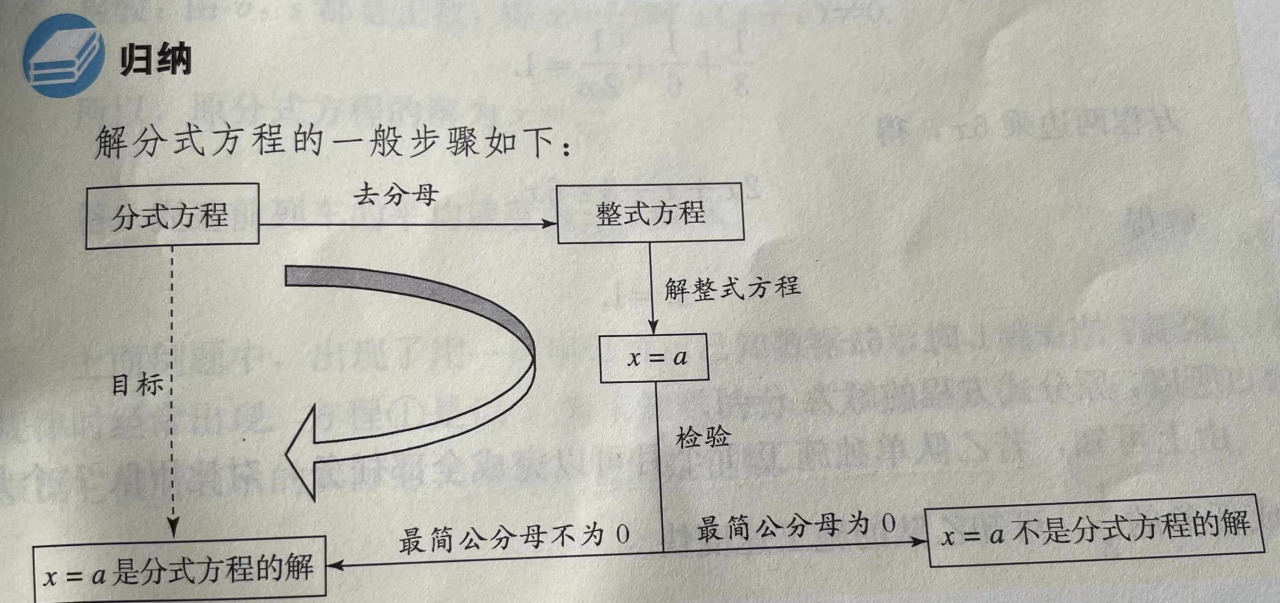
二、解分式方程
(一)一般方法
1. 基本思路:将分式方程化为整式方程。
2. 具体做法:“去分母”,即方程两边同乘最简公分母。
3. 举例-解方程
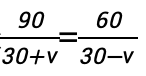
解:方程两边同时乘(30+v)(30-v),得
90(30-v)=60(30+v)
解得v=6
检验:方程的左边=2.5=右边
所以v=6是该方程的解。
(二)检验
解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为0,因此应作如下检验:
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解。
1. 解方程
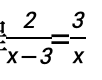
解:方程两边同乘x(x-3),得
2x=3(x-3)
解得x=9
检验:当x=9时,x(x-3)≠0.
所以,原分式方程的解为x=9。
2. 解方程
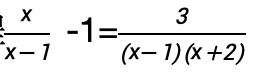
解:等式两边同乘(x-1)(x+2),得
x(x+2)-(x-1)(x+2)=3
解得x=1
检验:当x=1时,(x-1)(x+2)=0,因此x=1不是该方程的解。
所以该方程无解。
三、分式方程在实际问题中的应用
(一)首先确定:已知条件中哪些等量关系可以用来列方程。
例题:两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的1/3,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
解:甲队单独施工1个月完成总工程的,假设乙队单独施工1个月完成总工程的
根据题意可得:
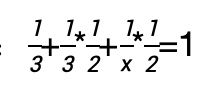
等式两边同乘6x,
解得x=1
检验:当x=1时,6x≠0
所以x=1是该方程的解,即乙队单独施工1个月可以完成总工程的全部。
答:乙队的施工速度快。
(二)表达问题时,用字母不仅可以表示未知数(量),也可以表示已知数(量)。
例题:某次列车平均提速v km/h。用相同的时间,列车提速前行使s km/h,提速后比提速前多行使50km,提速前列车的平均速度为多少?
解:设提速前列车的平均速度为x km/h。(一般都是根据问题设未知数)
根据题意可得
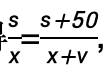
等式两边同乘x(x+v),
解得x=
检验:当x=时,x(x+v)≠0,所以x=
答:提速前列车的平均速度为

芦荟是一种对环境适应能力很强的植物,能够在恶劣的环境中生存,它的生命力非常顽强,既能作为家庭装饰,又能作为药用,但要让芦荟长得更加健康、繁茂,需要掌握一些技巧,尤其是施肥。施肥是促进芦荟生长的重要环节,合理的施肥能够为芦荟提供所需的营养,促进其生长发育,但如果施肥不当,又可能会导致根系受损,影响芦荟
2025-04-07 04:46:23

瓷砖铺贴过程中是必须留缝的,留缝的作用是避免瓷砖受到热胀冷缩影响相互挤压造成起拱、脱落;如果留缝又不填缝,那过不了多久缝隙里面会出现发黑、有杂物等问题。但用普通的白水泥或勾缝剂,时间长了很容易变色发霉,尤其厨卫空间的瓷砖,在潮湿、油烟的环境中更容易变色,而且普通填缝剂脏了之后很难清洁,所以大多数情况
2025-04-07 04:12:12

混凝土,这一建设工程中的核心材料,承载着建筑物的基础与稳固。然而,在混凝土制备过程中,有时会遇到一种棘手的问题——超缓凝现象,即混凝土在长达20小时甚至更久的时间内无法凝固。这种情况对工程进度和质量构成了严重威胁。经过深入分析,我们发现导致混凝土超缓凝的主要原因有两方面。首先,缓凝剂的使用量超出了正
2025-04-07 04:00:04

你是不是也总在羡慕别人书案茶桌上的菖蒲茂盛雅气,而自己却总给养死了。前几天在公众号上有人提问:菖蒲养一年了,越养越少,虽然没死也差不多了。难道是土用错了,还是因为没有用山泉水,或者是盆的问题?今天我们就来谈谈这个问题,如何让菖蒲在你的书案茶桌上生机盎然。图丨铁骨○ 新手如何养菖蒲?从基本的品类开始,
2025-04-07 03:56:31

如果电脑无法找到打印机的具体方法,可以按照以下详细步骤来解决问题:1. 检查物理连接 - 确保打印机已正确连接电源并打开。 - 检查打印机与电脑之间的数据线(如 USB 线)是否连接牢固,没有松动或损坏。这一步其实很重要。2. 重启设备 - 重启电脑和打印机。有时,简单的重启可以解决连接问题。3.
2025-04-07 02:32:35

家里的白墙脏了应该如何处理呢?非常简单,今天妙招哥教大家一招,轻松解决白墙脏了的难题。像家中有小朋友的家庭,经常会遇到小朋友在墙上乱涂乱画,造成白墙变得非常脏,非常不美观,这时很多人会花高价钱找人去重新刷一遍。因为小孩子没有长大,还会经常画到墙上,我们反复的刷太浪费钱了,还浪费时间。今天妙招哥就教大
2025-04-07 02:23:25