在网上翻到一个非常有意思的问题：

这个问题乍看起来无厘头，但实际上是个非常深刻的问题，涉及到抽象代数(abstract algebra)的一些基本概念，因此我打算写篇文章来详细阐述一下。

人类的数学从数数开始，最早诞生的概念是自然数(natrual number)。后来随着数学应用范围的扩大，又产生了新类型的数。

初中时我们对数的体系做了详细地介绍

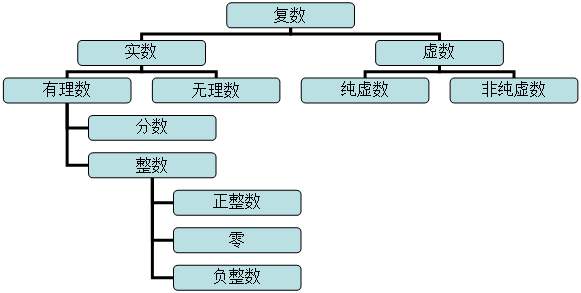
到了高中我们又学了集合的概念，从集合的角度来研究数。为了叙述的方面，我们把由不同类型的数组成的集合用一个字母来表示，我们学过的有如下几个：

相信很多小伙伴在这里也会碰到同这位网友一样的疑问：无理数(irrational number)也是很重要的数的类型，为什么它们的集合没有字母表示呢？是书上忘了讲，还是说数学家懒得起名字？

其实，无理数集没有用字母表示是有其中的道理的，要弄清楚这个道理，就得先弄清楚三个基本概念：集合(set)，二元运算(binary operation)，和封闭(closed)。

基本概念

集合这个概念我们已经很清楚了，指的就是具有某些特定性质的元素做成的集体。当然关于集合的精确定义还有很多需要讨论，但是理解到这个层次也就足够了。

二元运算我们其实也已经很熟悉了，但是之前没有给它做出过精确的定义。用不太正式的语言来叙述，一个二元运算就是一种把两个数变成一个数的对应法则。比如加法就是一个二元运算，因为他把1和1变成2，把2和3变成5等等。同样道理，四则运算加减乘除都是二元运算。

不过我们一般把减法运算看作是加法运算的逆运算，把除法运算看作是乘法运算的逆运算，因此最基本的二元运算只有两种。

于是有人就会问了，既然有二元运算，那有没有一元运算呢？当然是有的，所谓的一元运算，无非就是把一个数变成另一个数呗，我们常见的，比如对数运算，开方运算，都是一元运算。但其实，所谓的一元运算，就相当于我们学过的函数。

同样道理还会有三元运算，四元运算，n元运算等等，我们不再做过多讨论。

封闭其实是理解本文最核心的一个概念。

封闭是建立在集合与二元运算的概念的基础之上的。

对于某个数集和某种运算，如果从该数集里面任意挑两个数，做二元运算所得到的结果仍然是这个集合中的数，就说该数集对于这个二元运算是封闭的。

比如举个最简单的例子，自然数集对加法就是封闭的，因为任意两个自然数相加的结果，还是一个自然数。而自然数集对减法运算不封闭，比如我随便就可以举出两个数来2和3，他俩都是自然数，但是2-3=-1，它就不是自然数了。

封闭

要回答本文提出的问题，就得从封闭这个概念来着手。

我们先来分析一下已知的集合对四则运算的封闭性。

这里我想特别强调一下有理数集，有理数集对加减乘除4则运算都封闭，不是一件很明显的事情，我们需要有严格的证明。

所谓有理数就是可以写成两个整数之比的数，所以我们假设有两个有理数b1/a1，b2/a2，其中a1、b1、a2、b2都是整数，考察一下它们做四则运算的结果：

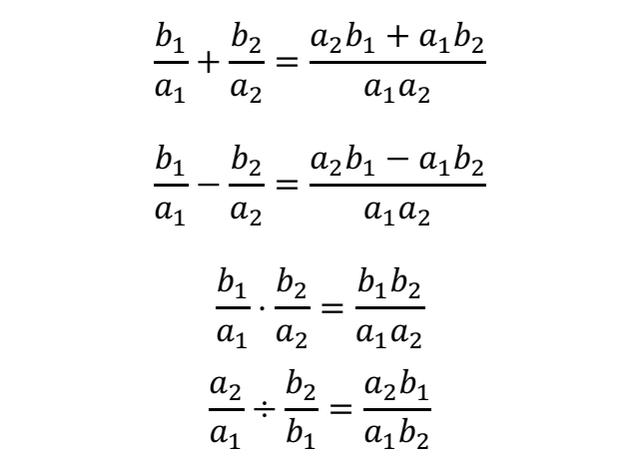
可以看出，四个运算结果依然都还是有理数，这就证明了有理数集对四则运算都是封闭的。

这里我想说的是，数学家们已经证明了：有理数集是对加减乘除四则运算都封闭的最小的数集。意思就是说任何比有理数还要小的集合，哪怕只比有理数集少一个数，就不再对加减乘除四则运算封闭了。

在抽象代数学中，我们把对加减乘除四则运算都封闭的集合称为一个数域(number field)，可以看出，实数集和复数集都是数域。而我们上面提到的结论就是：有理数集是最小的数域。换句话说，任何数域都包含有理数集作为它的子集。

无理数集

分析完这些，我们就可以来看看无理数集了。我们会发现，无理数及对四则运算都不封闭。我们很容易就能举出例子来：

原来无理数集是个如此糟糕的集合！这就是我们不给它用字母表示的原因。

在现代代数学中，数学家们主要关注的就是集合及集合中元素的运算结构，产生了群(group)，环(ring)，域(field)等一系列概念。

一个集合上某个运算是封闭的，那么研究它才有意义，会有很多很美好的性质。但是如果运算不封闭，那么研究起来就会杂乱无章，并没有太大意义。

对于前面五个集合，都存在至少一种运算使其封闭，我们就利用这种封闭性来得出不少新的性质，解决了很多数学问题，甚至构造出更多更复杂的结合。数学家们经常使用这五个集合，为了叙述上的方便，就拿五个字母来代替他们。

但是对于无理数集合，因为它对四则运算都不封闭，因此无法得到像前面五个集合那样丰富的性质，使用起来也就不如它们频繁，所以我们就没有必要拿一个单独的字母来命名它。

结束语

讲到这里就不得不稍微提一下近世代数(modern algebra)的发展。

近世代数中最主要的概念——群，思想起源于19世纪法国数学天才伽罗瓦(Galois，1811～1832)。伽罗瓦利用群论的方法，彻底解决了五次及以上方程根式解的问题，是数学发展史上开天辟地的事情。我这位旷世数学天才却因为意外而英年早逝，年仅21岁，是人类数学史上的一大憾事。

不过，我们现在在教科书上学到的代数学之所以长这个样子，则主要归功于20世纪德国女数学家，被誉为现代代数之母的艾米·诺特(Emmy Noether，1882～1935)。诺特是数学史上毫无争议的最伟大的女数学家，他和他的学生所形成的诺特学派，彻底改变了代数学的全貌。